2017华杯赛决赛准确答案出炉，多少分能得一二三等奖

第22届华杯赛初赛成都赛区考试已经落下帷幕，极客数学帮已经在考试后进行独家首发，现做正式汇总发布。在此之前，先解答大家最关心的两个问题。

（1）多少分进决赛？

整体来说本届华杯赛初赛难度和去年差不多，去年小中组40分进决赛，小高组50分进决赛，但也仅供参考，请以最终结果为准

第十四届华杯赛决赛答案（初中组）

第十四届华杯赛决赛答案（初中组）A卷答案：

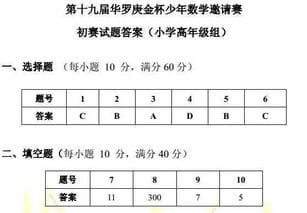
1、94/9 2、2（a-b) 3、3n 4、3.75

5、选2 6、－2.5≤m+n≤10.3

7、3又1003/1004 8、34

9、19≤x≤19又1/3 10、9

11、6 12、1又123/128

13、1740 14、(a+b)d2(此处2是d的平方，因打不出）/2(c+d)(ad+bc+2bd)

2010第15届华杯赛(初中组)决赛试题及答案

第十五届华罗庚金杯少年数学邀请赛决赛试题A（初一组）

（时间: 2010年4月10日10:00～11:30）

一、填空题 (每题10分, 共80分)

1.互不相等的有理数a, b, c在数轴上的对应点分别为A, B, C. 如果 ,那么在点A, B, C中, 居中的是点 .

2.右图所示的立体图形由9个棱长为1的正方体木块搭成,

这个立体图形的表面积为 .

3.汽车A从甲站出发开往乙站, 同时汽车B、C从乙站出发与A相向而行开往甲站, 途中A与B相遇后15分钟再与C相遇. 已知 A、B、C 的速度分别是每小时90km, 80km, 70km, 那么甲乙两站的路程是 km.

4.把自然数 分组, 要求每组内任3个数的最大公约数为1,则至少需分成 组.

5.已知正n边形的内角度数的两倍为整数, 那么这样的正整数n有 个.

6.已知 , 则 的值等于 .

7.六人参加乒乓球比赛, 每两人赛一场, 分胜负, 无平局. 最终他们胜的场数分别是a, b, b, c, d, d, 且 , 那么a等于 .

8.某中学新建游泳池开启使用, 先用一天时间匀速将空游泳池注满, 经两天的处理后同速将水放光; 然后开始同速注水, 注满一半时, 将注水速度加倍直到注满. 请在下图中用图表示游泳池中水量随时间的变化关系.

二、解答下列各题 (每题10分, 共40分, 要求写出简要过程)

9.能否找到7个整数, 使得这7个整数沿圆周排成一圈后, 任3个相

邻数的和都等29 ? 如果能, 请举一例. 如果不能, 请简述理由.

10.已知k 是满足 的整数, 并且使二元一次方程组 有整数解. 问: 这样的整数k有多少个?

11.所有以质数p为分母的最简真分数的和记为m, 所有以质数 q为分母的最简真分数的和记为n. 若 , 求 的可能值.

12.解方程 ,其中 [x] 表示不大于x的最大整数.

三、解答下列各题 (每题15分, 共30分, 要求写出详细过程)

13.右图中, ABC, BCD, CDE, DEF, EFA, FAB的面积之和等于六边形ABCDEF的面积. 又图中的6个阴影三角形面积之和等于六边形ABCDEF的面积的 . 求六边形 的面积与六边形ABCDEF的面积之比.

14.一个单项式加上多项式 后等于一个整式的平方, 试求所有这样的单项式.